
Missende, of ontbrekende, data wordt gedefinieerd als waardes die binnen een observatie voor een bepaalde variabele, niet zijn opgeslagen. Zoals in mijn vorige blog ook vermeld, is missende data een veelvoorkomend kwaliteitsprobleem wat het kan leiden tot ongunstige effecten, zoals een verminderde statistische kracht van de analyse, vertekening (bias) van verschillende statistische parameters en een afname in de mate waarin jouw data de werkelijkheid beschrijft1. Dit alles vergroot de kans op foutieve conclusies2.
Laten we een simpel voorbeeld bekijken met een aantal numerieke waardes in een multivariate dataset. Je hebt de temperatuur (in °C) en luchtvochtigheid (in %) op drie verschillende dagen gemeten en hebt de waardes in een dataset staan (A).
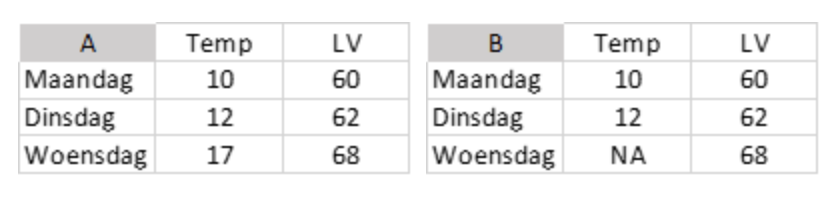
De gemiddelde middagtemperatuur over deze drie dagen is 13 graden. Maar stel dat nu de temperatuur van de laatste dag ontbreekt zoals in B, wat kun je dan doen? Wanneer je het gemiddelde van de temperatuur alsnog probeert te berekenen in R zul je ook NA terugkrijgen, omdat de waarde ongedefinieerd is. Je kunt dit oplossen door R te instrueren eventuele missende waardes te verwijderen voordat het gemiddelde wordt berekend. Doe je dit, dan rolt er netjes een gemiddelde van 11.5 graden uit. Een van de problemen hiermee is dat je in feite de gemiddelde temperatuur van alleen maandag en dinsdag hebt berekend zonder dat dit duidelijk is in de berekening. En wanneer je later de gemiddelde luchtvochtigheid berekend, kun je dan alle drie de dagen gebruiken of moet je ook hier de waarde van woensdag buiten beschouwing laten? Om het probleem met missende data te verhelpen zijn veel mensen geneigd om dan maar de hele observatie (of entry) te verwijderen. Maar wat zijn de gevolgen hiervan? En wat zijn de alternatieven?
Vormen van missende data
Om deze vragen te beantwoorden moeten we eerst kijken naar de manier waarop data kan ontbreken. Dit is in een aantal categorieën te plaatsen en welke bij jou van toepassing is heeft gevolgen voor de aanpak die je kunt gebruiken.
MCAR
De minst complexe vorm van missende data is wanneer elke waarde in de dataset (of binnen een variabele) dezelfde kans heeft om te ontbreken. Het maakt dus niet uit wat voor data het is of waar de waarde voorkomt, overal zul je willekeurig NA’s tegenkomen. Dit heet MCAR, missing completely at random. Omdat waardes overal kunnen missen, dus willekeurig verspreid over de hele dataset, geeft dit probleem geen vertekening van statistische parameters naar een bepaalde kant. In de voorbeeld data zou dit bijvoorbeeld kunnen gebeuren wanneer de batterijen van de temperatuursensor een aantal keer zijn uitgevallen. Deze momenten zijn willekeurig met betrekking tot de data die nu ontbreekt Het is dan niet mogelijk om een extra positief of negatief effect/relatie (bias) te zien vergeleken met van de originele data. Wel zorgt het, zoals eigenlijk elke vorm van missende data, voor minder kracht in data analyse door een afname van datapunten. Het is belangrijk te vermelden dan MCAR data in de praktijk weinig voorkomt; de manier waarop data wordt verzameld laat simpelweg weinig ruimte over voor willekeurige processen.
MAR
Daarnaast is het mogelijk dat de kans dat de verzamelde waardes missen wel afhangt van de observatie zelf. Dit wil zeggen dat de waardes niet meer willekeurig verspreid over de dataset missen maar, afhankelijk van eigenschappen horende bij de observatie, meer kans hebben om te ontbreken. Dit soort data wordt missing at random (MAR) genoemd en zorgt, in tegenstelling tot MCAR, wel tot een vertekend beeld van de data. Het gemiddelde van een variabele kan een stuk lager uitvallen wanneer juist de hoge waardes een grote kans hebben om te ontbreken (door een onbekende relatie van deze hoge waardes met een andere variabele). Hier kan dus wel sprake zijn van bias in de data en dit zorgt voor veel problemen met verdere analyse en kan leiden tot verkeerde conclusies.
MNA
Wanneer missende data niet in de MCAR of MAR categorie vallen, dan zijn ze MNAR, missing not at random. Dit betekent dat de kans dat bepaalde waardes ontbreken, afhankelijk is van een eigenschap die ons niet duidelijk is, maar in ieder geval niet willekeurig. Dit is problematisch omdat je in dit geval niet kunt weten wat de beste manier is om alsnog iets over de ontbrekende waardes te weten te komen. Daarnaast gelden voor analyse van de data dezelfde limitaties als bij MAR data.
Het verschil tussen MAR en MNAR lijkt klein, maar is erg belangrijk voor de vervolgstappen die je kunt nemen. Bekijken we nog een keer het voorbeeld van de eerdere temperatuur- en vochtigheid metingen, zien we wat het verschil tussen de twee problemen betekent. Stel je voor dat de temperatuurmeter minder goed blijkt te werken bij een hoge luchtvochtigheid en om die reden af en toe een meting mist, dan is er sprake van MAR. De waarde temperatuur heeft tenslotte meer kans om te ontbreken afhankelijk van de waarde van een andere gemeten variabele – luchtvochtigheid. Omdat er van alle dagen een meting van de luchtvochtigheid is, kunnen we de temperatuur data nog enigszins inschatten, ervan uitgaande dat luchtvochtigheid en temperatuur gecorreleerd zijn. Als de temperatuursensor echter niet goed blijkt te werken wanneer deze te warm wordt en er daardoor meer waardes missen aan de bovenkant van de range dan in de rest van de waardes, dan kunnen deze waardes niet of slecht worden ingeschat op basis van de andere data. MNAR wordt daarom gezien als een groot probleem m.b.t. de kwaliteit van de data, waarbij vertekening van de data en bias in de resultaten gegarandeerd is2.
Impliciet en expliciet missende data
Tenslotte kan data ook nog impliciet of expliciet ontbreken. De tweede tabel (B) eerder in deze blog is een voorbeeld van expliciet missende data. Er staat namelijk een NA bij een van de variabelen, dus het is makkelijk te herkennen. Ook wanneer je dataset te groot is om alle waardes individueel te bekijken zijn er tal van mogelijkheden om missende waardes te vinden (zie hiervoor ook mijn vorige blog). Maar wat als de missende waardes niet aanwezig zijn in je dataset? Stel je voor dat je jouw eerder gemeten data wilt vergelijken met meteorologische data die je online hebt gevonden.
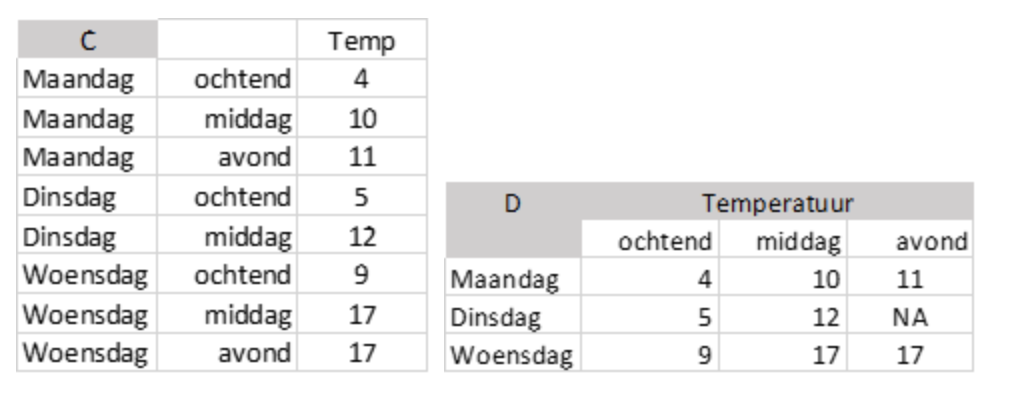
Wat opvalt is dat er voor dinsdag maar twee metingen zijn (tabel C), voor maandag en woensdag zijn dit er drie. Dit betekent dat je een missende, missende waarde hebt voor dinsdagavond. Dit wordt een impliciet missende waarde genoemd. Je kunt deze dan beter weergeven zoals in tabel D, zodat het duidelijk is of en welke data mist. Wanneer je bijvoorbeeld een gemiddelde dagtemperatuur wilt berekenen en de drie dagen wilt vergelijken zul je rekening moeten houden met het feit dat je voor dinsdagavond geen waarde hebt. Je kunt daardoor niet zomaar de vergelijking maken met de andere dagen, waar er wel een temperatuur is gemeten voor de avond. Je kunt hier beslissen om analyses alleen uit te voeren op observaties die compleet zijn, in dit geval maandag en dinsdag. Dit wordt complete case analysis genoemd en is eigenlijk de standaard manier om met missende data om te gaan. Maar het zorgt in sommige gevallen voor een vertekend beeld van je data en onjuiste conclusies doordat je mogelijk waardevolle data buiten beschouwing laat.
Het vervangen van NA
Laten we nu kijken naar een aantal methoden die je helpen om te gaan met missende data. Het doel van iedere methode is het elimineren of vervangen van missende data, zodat er analyses kunnen worden uitgevoerd. Dit is maar een klein deel van alle methoden en per methode bestaan vaak verschillende variaties, afhankelijk van het vakgebied en de vorm van (missende) data.
Listwise deletion
Deze methode is in de praktijk gelijk aan complete case analysis en houdt in dat je de hele observatie verwijdert uit je dataset, wanneer er minimaal één variabele mist. In tegenstelling tot complete case analysis heb je hier de gehele observatie verwijderd en ben je deze dus kwijt wanneer je andere variabelen wilt analyseren. In het voorbeeld van tabel D, verlies je de ochtend en middag temperatuur van dinsdag en hou je alleen de waardes horende bij maandag en woensdag over. Wanneer je data MCAR is, is dit een simpele en relatief veilige optie omdat je de data niet vertekend (de missende data was tenslotte willekeurig verdeeld over je dataset, en dus de verwijderde data ook). Wanneer je data MAR of MNAR is, kan dat wel het geval zijn en moet je uitkijken met het zomaar verwijderen van data. Ook bij kleine datasets kan het niet wenselijk zijn om data te verwijderen, er zal simpelweg minder data overblijven om statistische verschillen te ontdekken.
Last observation carried forward
Wanneer je werkt met sequentiële data, bijvoorbeeld een tijd series, kan deze methode een betere benadering geven van een missende waarde dan andere methoden. Het houdt namelijk rekening met de data als informatie door de tijd en deze zal zich ook zo gedragen; waardes liggen vaker in de buurt bij voorgaande of volgende waardes dan in niet sequentiële dataset. Zoals de naam impliceert, wordt elke missende waarde vervangen door de waarde van de voorgaande observatie. Dit is opnieuw een relatief simpele methode die makkelijk te interpreteren resultaten geeft. Het onderschat wel de variatie in de observaties en de inzetbaarheid moet kritisch worden bekeken. Het gebruik ervan hangt onder andere af van de hoeveelheid en vorm van de (missende) data. Om weer onze tabel D erbij te pakken; de missende waarde wordt dit keer vervangen door 11 (van maandagavond). We werken hier echter met erg weinig data en het is moeilijk te bepalen of dit nu een goede methode is.
Mean imputation
Imputation is het vervangen van missende data met berekende ‘schattingen’. Er zijn tal van mogelijkheden om een waarde te schatten en bij mean imputation (of mean substitution) wordt een missende waarde vervangen door het gemiddelde van de kolom waarin de waarde is gevonden. In onze tabel D zou de NA vervangen worden door het gemiddelde van de overige avondtemperatuur waardes, wat op 14 uitkomt. Dit zorgt ervoor dat de dinsdag behouden kan worden, waardoor in theorie meer analyses uitgevoerd kunnen worden met meer data. De achterliggende gedachte is dat het gemiddelde de beste schatting is van de oorspronkelijke waarde (bij een normale distributie). Maar dit gemiddelde is per definitie niet willekeurig en dat zorgt voor vertekening van statistische parameters, met name de afname van de standaardafwijking. Ook zorgt de nieuwe waarde niet voor nieuwe informatie in de dataset.
Regression imputation
Regression imputation is een voorbeeld waarbij niet-missende waardes worden gebruikt om een regressie model op te stellen. Je hebt hier vanzelfsprekend minimaal 2 variabelen voor nodig. De missende waardes worden geschat op basis van dit model, waarbij de waardes op de regressielijn liggen – de fitted value dus. Ook deze waarde is niet willekeurig; het gebruik van de methode draagt bij aan het overschatten van relaties tussen variabelen en suggereert hogere precisie in de data dan in werkelijkheid het geval is.
Om regression imputation bruikbaarder te maken zijn er verschillende variaties bedacht op deze methode3. Zo is het mogelijk om de standaarddeviatie van de aanwezige data te gebruiken om onzekerheid in te brengen bij de geschatte waardes, zodat ze op een normale distributie rond de regressielijn terecht komen. Hierdoor wordt de variatie in de data deels behouden en relaties tussen de variabelen minder sterk overschat. Vaak bevat een dataset nog andere variabelen die gebruikt kunnen worden om nog betere schattingen te kunnen maken.
Multiple imputation
Bij Multiple imputation (MI) worden meerdere schattingen van de missende waarde(s) gemaakt op basis van de wel aanwezige data. Deze geschatte waardes kunnen op verschillende manieren tot stand komen, er zijn dus meer vormen van MI mogelijk. De gevonden waardes worden gecombineerd met de originele dataset en vervolgens worden verschillende, complete, datasets gegenereerd, die op hun beurt kunnen worden geanalyseerd. Zo is deze methode in staat om, In tegenstelling tot single imputation (e.g. mean substitution en regression imputation), de onzekerheid over de geschatte waardes te laten blijken door simpelweg niet te doen alsof er één de juiste is. Deze methode wordt gezien als een van de meer robuuste manieren om missende data te vervangen en is goed in staat om problemen met de vertekening van de data, en statistische parameters zoals de standaard afwijking, te voorkomen. MI werkt ook goed met een kleine dataset, of wanneer er veel data mist.
Maximum likelihood
Bij deze methode wordt op basis van de aanwezige data een schatting gemaakt van de parameters die een kansverdeling beschrijven die op zijn beurt het beste te matchen is met de verdeling van de data. In veruit de meeste gevallen is maximum likelihood (ML) methode een iteratief proces waarbij de parameters na vele herberekeningen op de beste parameters uitkomen4. Vanuit die verdeling worden (willekeurig) de missende waardes vervangen met nieuwe waardes. Ook hier treedt een relatief lage vertekening van de data op en zal de natuurlijke variatie in de data ook in de nieuwe waardes aanwezig zijn.
Tot slot
Om uiteindelijk een idee te krijgen van de impact van jouw missende data, raad ik je aan om een sensitivy analysis uit te voeren. In veel vakgebieden zijn er standaarden waarop je dit kunt doen. Het proces komt neer op het aanpassen van de invoer waardes van je analyse om vervolgens de uitkomsten te vergelijken. Zo kun je verschillende geschatte waardes als invoer gebruiken om te zien hoe groot de variatie in je uitkomsten is; in andere woorden dus hoe gevoelig je model is. Lage gevoeligheid wil over het algemeen zeggen dat je analyse beter is bestand tegen de onzekerheid in de geschatte waardes en je dus minder effect zult ondervinden van je missende data. De uitkomsten van Multiple Imputation, in de vorm van meerdere datasets, lenen zich bijvoorbeeld goed voor zo’n analyse.
Het probleem van missende data is niet zozeer de extra stappen die je moet doen om de data bruikbaar te maken. Het gevaar zit hem in het overschatten van de nieuwe, complete, data. Het is makkelijk te vergeten dat de geschatte waardes altijd een mate van onzekerheid met zich meebrengen, ze kunnen onmogelijk juist zijn! Elke waarde in elke dataset is een observatie, gedaan in de echte wereld. Als deze waarde mist, is er maar één manier om de juiste waarde te achterhalen en dat is door precies dezelfde observatie of meting opnieuw uit te voeren.
Referenties:
- Kang H. (2013). The prevention and handling of the missing data. Korean journal of anesthesiology, 64(5), 402–406. https://doi.org/10.4097/kjae.2013.64.5.402
- Graham, J. W. (2009). Missing Data Analysis: Making It Work in the Real World. Annual Review of Psychology, 60(1), 549–576. doi:10.1146/annurev.psych.58.110405.085530
- van Buuren, S. (2018). Flexible Imputation of Missing Data, Second Edition. New York: Chapman and Hall/CRC, https://doi.org/10.1201/9780429492259 https://stefvanbuuren.name/fimd/
- Von Hippel, P. T. (2015). New Confidence Intervals and Bias Comparisons Show That Maximum Likelihood Can Beat Multiple Imputation in Small Samples. Structural Equation Modeling: A Multidisciplinary Journal, 23(3), 422–437. doi:10.1080/10705511.2015.1047931



